|
Test of Time Award
|
[ Hall F ]
Test of Time Award:Poisoning Attacks Against Support Vector Machines Battista Biggio, Blaine Nelson, Pavel Laskov: Test of Time Honorable Mention:Building high-level features using large scale unsupervised learning Quoc Le, Marc'Aurelio Ranzato, Rajat Monga, Matthieu Devin, Kai Chen, Greg Corrado, Jeff Dean, Andrew Ng On causal and anticausal learning Bernhard Schölkopf, Dominik Janzing, Jonas Peters, Eleni Sgouritsa, Kun Zhang, Joris Mooij |
|
Outstanding Paper
|
[ Ballroom 3 & 4 ] 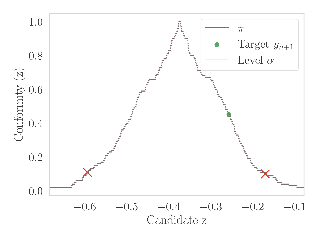
When one observes a sequence of variables $(x_1, y_1), \ldots, (x_n, y_n)$, Conformal Prediction (CP) is a methodology that allows to estimate a confidence set for $y_{n+1}$ given $x_{n+1}$ by merely assuming that the distribution of the data is exchangeable. CP sets have guaranteed coverage for any finite population size $n$. While appealing, the computation of such a set turns out to be infeasible in general, \eg when the unknown variable $y_{n+1}$ is continuous. The bottleneck is that it is based on a procedure that readjusts a prediction model on data where we replace the unknown target by all its possible values in order to select the most probable one. This requires computing an infinite number of models, which often makes it intractable. In this paper, we combine CP techniques with classical algorithmic stability bounds to derive a prediction set computable with a single model fit. We demonstrate that our proposed confidence set does not lose any coverage guarantees while avoiding the need for data splitting as currently done in the literature. We provide some numerical experiments to illustrate the tightness of our estimation when the sample size is sufficiently large, on both synthetic and real datasets.
|
|
Outstanding Paper
|
[ Room 318 - 320 ] 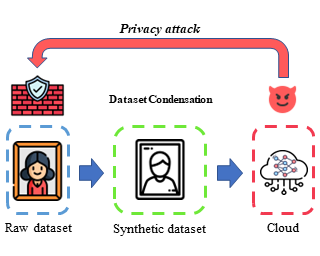
To prevent unintentional data leakage, research community has resorted to data generators that can produce differentially private data for model training. However, for the sake of the data privacy, existing solutions suffer from either expensive training cost or poor generalization performance. Therefore, we raise the question whether training efficiency and privacy can be achieved simultaneously. In this work, we for the first time identify that dataset condensation (DC) which is originally designed for improving training efficiency is also a better solution to replace the traditional data generators for private data generation, thus providing privacy for free. To demonstrate the privacy benefit of DC, we build a connection between DC and differential privacy, and theoretically prove on linear feature extractors (and then extended to non-linear feature extractors) that the existence of one sample has limited impact ($O(m/n)$) on the parameter distribution of networks trained on $m$ samples synthesized from $n (n \gg m)$ raw samples by DC. We also empirically validate the visual privacy and membership privacy of DC-synthesized data by launching both the loss-based and the state-of-the-art likelihood-based membership inference attacks. We envision this work as a milestone for data-efficient and privacy-preserving machine learning.
|
|
Outstanding Paper
|
[ Room 307 ] 
Recent work highlights the role of causality in designing equitable decision-making algorithms. It is not immediately clear, however, how existing causal conceptions of fairness relate to one another, or what the consequences are of using these definitions as design principles. Here, we first assemble and categorize popular causal definitions of algorithmic fairness into two broad families: (1) those that constrain the effects of decisions on counterfactual disparities; and (2) those that constrain the effects of legally protected characteristics, like race and gender, on decisions. We then show, analytically and empirically, that both families of definitions \emph{almost always}---in a measure theoretic sense---result in strongly Pareto dominated decision policies, meaning there is an alternative, unconstrained policy favored by every stakeholder with preferences drawn from a large, natural class. For example, in the case of college admissions decisions, policies constrained to satisfy causal fairness definitions would be disfavored by every stakeholder with neutral or positive preferences for both academic preparedness and diversity.Indeed, under a prominent definition of causal fairness, we prove the resulting policies require admitting all students with the same probability, regardless of academic qualifications or group membership. Our results highlight formal limitations and potential adverse consequences of common mathematical notions of … |
|
Outstanding Paper
|
[ Hall E ] 
Recent work highlights the role of causality in designing equitable decision-making algorithms. It is not immediately clear, however, how existing causal conceptions of fairness relate to one another, or what the consequences are of using these definitions as design principles. Here, we first assemble and categorize popular causal definitions of algorithmic fairness into two broad families: (1) those that constrain the effects of decisions on counterfactual disparities; and (2) those that constrain the effects of legally protected characteristics, like race and gender, on decisions. We then show, analytically and empirically, that both families of definitions \emph{almost always}---in a measure theoretic sense---result in strongly Pareto dominated decision policies, meaning there is an alternative, unconstrained policy favored by every stakeholder with preferences drawn from a large, natural class. For example, in the case of college admissions decisions, policies constrained to satisfy causal fairness definitions would be disfavored by every stakeholder with neutral or positive preferences for both academic preparedness and diversity.Indeed, under a prominent definition of causal fairness, we prove the resulting policies require admitting all students with the same probability, regardless of academic qualifications or group membership. Our results highlight formal limitations and potential adverse consequences of common mathematical notions of … |
|
Outstanding Paper
|
[ Room 301 - 303 ] 
Estimating the difficulty of a dataset typically involves comparing state-of-the-art models to humans; the bigger the performance gap, the harder the dataset is said to be. However, this comparison provides little understanding of how difficult each instance in a given distribution is, or what attributes make the dataset difficult for a given model. To address these questions, we frame dataset difficulty---w.r.t. a model $\mathcal{V}$---as the lack of $\mathcal{V}$-usable information (Xu et al., 2019), where a lower value indicates a more difficult dataset for $\mathcal{V}$. We further introduce pointwise $\mathcal{V}$-information (PVI) for measuring the difficulty of individual instances w.r.t. a given distribution. While standard evaluation metrics typically only compare different models for the same dataset, $\mathcal{V}$-usable information and PVI also permit the converse: for a given model $\mathcal{V}$, we can compare different datasets, as well as different instances/slices of the same dataset. Furthermore, our framework allows for the interpretability of different input attributes via transformations of the input, which we use to discover annotation artefacts in widely-used NLP benchmarks.
|
|
Outstanding Paper
|
[ Hall E ] 
To prevent unintentional data leakage, research community has resorted to data generators that can produce differentially private data for model training. However, for the sake of the data privacy, existing solutions suffer from either expensive training cost or poor generalization performance. Therefore, we raise the question whether training efficiency and privacy can be achieved simultaneously. In this work, we for the first time identify that dataset condensation (DC) which is originally designed for improving training efficiency is also a better solution to replace the traditional data generators for private data generation, thus providing privacy for free. To demonstrate the privacy benefit of DC, we build a connection between DC and differential privacy, and theoretically prove on linear feature extractors (and then extended to non-linear feature extractors) that the existence of one sample has limited impact ($O(m/n)$) on the parameter distribution of networks trained on $m$ samples synthesized from $n (n \gg m)$ raw samples by DC. We also empirically validate the visual privacy and membership privacy of DC-synthesized data by launching both the loss-based and the state-of-the-art likelihood-based membership inference attacks. We envision this work as a milestone for data-efficient and privacy-preserving machine learning.
|
|
Outstanding Paper
|
[ Hall E ] 
Estimating the difficulty of a dataset typically involves comparing state-of-the-art models to humans; the bigger the performance gap, the harder the dataset is said to be. However, this comparison provides little understanding of how difficult each instance in a given distribution is, or what attributes make the dataset difficult for a given model. To address these questions, we frame dataset difficulty---w.r.t. a model $\mathcal{V}$---as the lack of $\mathcal{V}$-usable information (Xu et al., 2019), where a lower value indicates a more difficult dataset for $\mathcal{V}$. We further introduce pointwise $\mathcal{V}$-information (PVI) for measuring the difficulty of individual instances w.r.t. a given distribution. While standard evaluation metrics typically only compare different models for the same dataset, $\mathcal{V}$-usable information and PVI also permit the converse: for a given model $\mathcal{V}$, we can compare different datasets, as well as different instances/slices of the same dataset. Furthermore, our framework allows for the interpretability of different input attributes via transformations of the input, which we use to discover annotation artefacts in widely-used NLP benchmarks.
|
|
Outstanding Paper
|
[ Hall E ] 
In the maximum state entropy exploration framework, an agent interacts with a reward-free environment to learn a policy that maximizes the entropy of the expected state visitations it is inducing. Hazan et al. (2019) noted that the class of Markovian stochastic policies is sufficient for the maximum state entropy objective, and exploiting non-Markovianity is generally considered pointless in this setting. In this paper, we argue that non-Markovianity is instead paramount for maximum state entropy exploration in a finite-sample regime. Especially, we recast the objective to target the expected entropy of the induced state visitations in a single trial. Then, we show that the class of non-Markovian deterministic policies is sufficient for the introduced objective, while Markovian policies suffer non-zero regret in general. However, we prove that the problem of finding an optimal non-Markovian policy is NP-hard. Despite this negative result, we discuss avenues to address the problem in a tractable way and how non-Markovian exploration could benefit the sample efficiency of online reinforcement learning in future works. |
|
Outstanding Paper
|
[ Hall G ] 
We study the problem of learning a mixture of multiple linear dynamical systems (LDSs) from unlabeled short sample trajectories, each generated by one of the LDS models. Despite the wide applicability of mixture models for time-series data, learning algorithms that come with end-to-end performance guarantees are largely absent from existing literature. There are multiple sources of technical challenges, including but not limited to (1) the presence of latent variables (i.e. the unknown labels of trajectories); (2) the possibility that the sample trajectories might have lengths much smaller than the dimension $d$ of the LDS models; and (3) the complicated temporal dependence inherent to time-series data. To tackle these challenges, we develop a two-stage meta-algorithm, which is guaranteed to efficiently recover each ground-truth LDS model up to error $\tilde{O}(\sqrt{d/T})$, where $T$ is the total sample size. We validate our theoretical studies with numerical experiments, confirming the efficacy of the proposed algorithm.
|
|
Outstanding Paper
|
[ Hall E ] 
The Stackelberg prediction game (SPG) is popular in characterizing strategic interactions between a learner and an attacker. As an important special case, the SPG with least squares loss (SPG-LS) has recently received much research attention. Although initially formulated as a difficult bi-level optimization problem, SPG-LS admits tractable reformulations which can be polynomially globally solved by semidefinite programming or second order cone programming. However, all the available approaches are not well-suited for handling large-scale datasets, especially those with huge numbers of features. In this paper, we explore an alternative reformulation of the SPG-LS. By a novel nonlinear change of variables, we rewrite the SPG-LS as a spherically constrained least squares (SCLS) problem. Theoretically, we show that an $\epsilon$ optimal solutions to the SCLS (and the SPG-LS) can be achieved in $\tilde O(N/\sqrt{\epsilon})$ floating-point operations, where $N$ is the number of nonzero entries in the data matrix. Practically, we apply two well-known methods for solving this new reformulation, i.e., the Krylov subspace method and the Riemannian trust region method. Both algorithms are factorization free so that they are suitable for solving large scale problems. Numerical results on both synthetic and real-world datasets indicate that the SPG-LS, equipped with the SCLS reformulation, can …
|
|
Outstanding Paper
|
[ Hall E ] 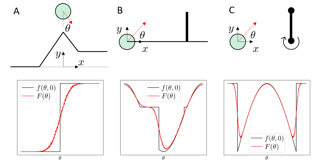
Differentiable simulators promise faster computation time for reinforcement learning by replacing zeroth-order gradient estimates of a stochastic objective with an estimate based on first-order gradients. However, it is yet unclear what factors decide the performance of the two estimators on complex landscapes that involve long-horizon planning and control on physical systems, despite the crucial relevance of this question for the utility of differentiable simulators. We show that characteristics of certain physical systems, such as stiffness or discontinuities, may compromise the efficacy of the first-order estimator, and analyze this phenomenon through the lens of bias and variance. We additionally propose an $\alpha$-order gradient estimator, with $\alpha \in [0,1]$, which correctly utilizes exact gradients to combine the efficiency of first-order estimates with the robustness of zero-order methods. We demonstrate the pitfalls of traditional estimators and the advantages of the $\alpha$-order estimator on some numerical examples.
|
|
Outstanding Paper
|
[ Hall E ] 
This work develops mixup for graph data. Mixup has shown superiority in improving the generalization and robustness of neural networks by interpolating features and labels between two random samples. Traditionally, Mixup can work on regular, grid-like, and Euclidean data such as image or tabular data. However, it is challenging to directly adopt Mixup to augment graph data because different graphs typically: 1) have different numbers of nodes; 2) are not readily aligned; and 3) have unique typologies in non-Euclidean space. To this end, we propose G-Mixup to augment graphs for graph classification by interpolating the generator (i.e., graphon) of different classes of graphs. Specifically, we first use graphs within the same class to estimate a graphon. Then, instead of directly manipulating graphs, we interpolate graphons of different classes in the Euclidean space to get mixed graphons, where the synthetic graphs are generated through sampling based on the mixed graphons. Extensive experiments show that G-Mixup substantially improves the generalization and robustness of GNNs. |
|
Outstanding Paper
|
[ Hall E ] 
When one observes a sequence of variables $(x_1, y_1), \ldots, (x_n, y_n)$, Conformal Prediction (CP) is a methodology that allows to estimate a confidence set for $y_{n+1}$ given $x_{n+1}$ by merely assuming that the distribution of the data is exchangeable. CP sets have guaranteed coverage for any finite population size $n$. While appealing, the computation of such a set turns out to be infeasible in general, \eg when the unknown variable $y_{n+1}$ is continuous. The bottleneck is that it is based on a procedure that readjusts a prediction model on data where we replace the unknown target by all its possible values in order to select the most probable one. This requires computing an infinite number of models, which often makes it intractable. In this paper, we combine CP techniques with classical algorithmic stability bounds to derive a prediction set computable with a single model fit. We demonstrate that our proposed confidence set does not lose any coverage guarantees while avoiding the need for data splitting as currently done in the literature. We provide some numerical experiments to illustrate the tightness of our estimation when the sample size is sufficiently large, on both synthetic and real datasets.
|
|
Outstanding Paper
|
[ Room 310 ] 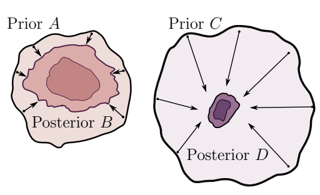
How do we compare between hypotheses that are entirely consistent with observations? The marginal likelihood (aka Bayesian evidence), which represents the probability of generating our observations from a prior, provides a distinctive approach to this foundational question, automatically encoding Occam's razor. Although it has been observed that the marginal likelihood can overfit and is sensitive to prior assumptions, its limitations for hyperparameter learning and discrete model comparison have not been thoroughly investigated. We first revisit the appealing properties of the marginal likelihood for learning constraints and hypothesis testing. We then highlight the conceptual and practical issues in using the marginal likelihood as a proxy for generalization. Namely, we show how marginal likelihood can be negatively correlated with generalization, with implications for neural architecture search, and can lead to both underfitting and overfitting in hyperparameter learning. We provide a partial remedy through a conditional marginal likelihood, which we show is more aligned with generalization, and practically valuable for large-scale hyperparameter learning, such as in deep kernel learning. |
|
Outstanding Paper
|
[ Hall E ] 
We study the problem of learning a mixture of multiple linear dynamical systems (LDSs) from unlabeled short sample trajectories, each generated by one of the LDS models. Despite the wide applicability of mixture models for time-series data, learning algorithms that come with end-to-end performance guarantees are largely absent from existing literature. There are multiple sources of technical challenges, including but not limited to (1) the presence of latent variables (i.e. the unknown labels of trajectories); (2) the possibility that the sample trajectories might have lengths much smaller than the dimension $d$ of the LDS models; and (3) the complicated temporal dependence inherent to time-series data. To tackle these challenges, we develop a two-stage meta-algorithm, which is guaranteed to efficiently recover each ground-truth LDS model up to error $\tilde{O}(\sqrt{d/T})$, where $T$ is the total sample size. We validate our theoretical studies with numerical experiments, confirming the efficacy of the proposed algorithm.
|
|
Outstanding Paper
|
[ Hall G ] 
Differentiable simulators promise faster computation time for reinforcement learning by replacing zeroth-order gradient estimates of a stochastic objective with an estimate based on first-order gradients. However, it is yet unclear what factors decide the performance of the two estimators on complex landscapes that involve long-horizon planning and control on physical systems, despite the crucial relevance of this question for the utility of differentiable simulators. We show that characteristics of certain physical systems, such as stiffness or discontinuities, may compromise the efficacy of the first-order estimator, and analyze this phenomenon through the lens of bias and variance. We additionally propose an $\alpha$-order gradient estimator, with $\alpha \in [0,1]$, which correctly utilizes exact gradients to combine the efficiency of first-order estimates with the robustness of zero-order methods. We demonstrate the pitfalls of traditional estimators and the advantages of the $\alpha$-order estimator on some numerical examples.
|
|
Outstanding Paper
|
[ Hall E ] 
How do we compare between hypotheses that are entirely consistent with observations? The marginal likelihood (aka Bayesian evidence), which represents the probability of generating our observations from a prior, provides a distinctive approach to this foundational question, automatically encoding Occam's razor. Although it has been observed that the marginal likelihood can overfit and is sensitive to prior assumptions, its limitations for hyperparameter learning and discrete model comparison have not been thoroughly investigated. We first revisit the appealing properties of the marginal likelihood for learning constraints and hypothesis testing. We then highlight the conceptual and practical issues in using the marginal likelihood as a proxy for generalization. Namely, we show how marginal likelihood can be negatively correlated with generalization, with implications for neural architecture search, and can lead to both underfitting and overfitting in hyperparameter learning. We provide a partial remedy through a conditional marginal likelihood, which we show is more aligned with generalization, and practically valuable for large-scale hyperparameter learning, such as in deep kernel learning. |
|
Outstanding Paper
|
[ Room 318 - 320 ] 
This work develops mixup for graph data. Mixup has shown superiority in improving the generalization and robustness of neural networks by interpolating features and labels between two random samples. Traditionally, Mixup can work on regular, grid-like, and Euclidean data such as image or tabular data. However, it is challenging to directly adopt Mixup to augment graph data because different graphs typically: 1) have different numbers of nodes; 2) are not readily aligned; and 3) have unique typologies in non-Euclidean space. To this end, we propose G-Mixup to augment graphs for graph classification by interpolating the generator (i.e., graphon) of different classes of graphs. Specifically, we first use graphs within the same class to estimate a graphon. Then, instead of directly manipulating graphs, we interpolate graphons of different classes in the Euclidean space to get mixed graphons, where the synthetic graphs are generated through sampling based on the mixed graphons. Extensive experiments show that G-Mixup substantially improves the generalization and robustness of GNNs. |
|
Outstanding Paper
|
[ Room 318 - 320 ] 
The Stackelberg prediction game (SPG) is popular in characterizing strategic interactions between a learner and an attacker. As an important special case, the SPG with least squares loss (SPG-LS) has recently received much research attention. Although initially formulated as a difficult bi-level optimization problem, SPG-LS admits tractable reformulations which can be polynomially globally solved by semidefinite programming or second order cone programming. However, all the available approaches are not well-suited for handling large-scale datasets, especially those with huge numbers of features. In this paper, we explore an alternative reformulation of the SPG-LS. By a novel nonlinear change of variables, we rewrite the SPG-LS as a spherically constrained least squares (SCLS) problem. Theoretically, we show that an $\epsilon$ optimal solutions to the SCLS (and the SPG-LS) can be achieved in $\tilde O(N/\sqrt{\epsilon})$ floating-point operations, where $N$ is the number of nonzero entries in the data matrix. Practically, we apply two well-known methods for solving this new reformulation, i.e., the Krylov subspace method and the Riemannian trust region method. Both algorithms are factorization free so that they are suitable for solving large scale problems. Numerical results on both synthetic and real-world datasets indicate that the SPG-LS, equipped with the SCLS reformulation, can …
|
|
Outstanding Paper
|
[ Hall G ] 
In the maximum state entropy exploration framework, an agent interacts with a reward-free environment to learn a policy that maximizes the entropy of the expected state visitations it is inducing. Hazan et al. (2019) noted that the class of Markovian stochastic policies is sufficient for the maximum state entropy objective, and exploiting non-Markovianity is generally considered pointless in this setting. In this paper, we argue that non-Markovianity is instead paramount for maximum state entropy exploration in a finite-sample regime. Especially, we recast the objective to target the expected entropy of the induced state visitations in a single trial. Then, we show that the class of non-Markovian deterministic policies is sufficient for the introduced objective, while Markovian policies suffer non-zero regret in general. However, we prove that the problem of finding an optimal non-Markovian policy is NP-hard. Despite this negative result, we discuss avenues to address the problem in a tractable way and how non-Markovian exploration could benefit the sample efficiency of online reinforcement learning in future works. |
|
Outstanding Paper Runner Up
|
[ Hall E ] 
We consider the problem of predicting a protein sequence from its backbone atom coordinates. Machine learning approaches to this problem to date have been limited by the number of available experimentally determined protein structures. We augment training data by nearly three orders of magnitude by predicting structures for 12M protein sequences using AlphaFold2. Trained with this additional data, a sequence-to-sequence transformer with invariant geometric input processing layers achieves 51% native sequence recovery on structurally held-out backbones with 72% recovery for buried residues, an overall improvement of almost 10 percentage points over existing methods. The model generalizes to a variety of more complex tasks including design of protein complexes, partially masked structures, binding interfaces, and multiple states. |
|
Outstanding Paper Runner Up
|
[ Room 301 - 303 ] 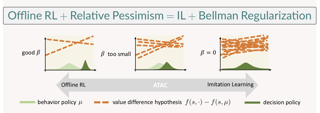
We propose Adversarially Trained Actor Critic (ATAC), a new model-free algorithm for offline reinforcement learning (RL) under insufficient data coverage, based on the concept of relative pessimism. ATAC is designed as a two-player Stackelberg game framing of offline RL: A policy actor competes against an adversarially trained value critic, who finds data-consistent scenarios where the actor is inferior to the data-collection behavior policy. We prove that, when the actor attains no regret in the two-player game, running ATAC produces a policy that provably 1) outperforms the behavior policy over a wide range of hyperparameters that control the degree of pessimism, and 2) competes with the best policy covered by data with appropriately chosen hyperparameters. Compared with existing works, notably our framework offers both theoretical guarantees for general function approximation and a deep RL implementation scalable to complex environments and large datasets. In the D4RL benchmark, ATAC consistently outperforms state-of-the-art offline RL algorithms on a range of continuous control tasks. |
|
Outstanding Paper Runner Up
|
[ Hall E ] 
The fast spreading adoption of machine learning (ML) by companies across industries poses significant regulatory challenges. One such challenge is scalability: how can regulatory bodies efficiently \emph{audit} these ML models, ensuring that they are fair? In this paper, we initiate the study of query-based auditing algorithms that can estimate the demographic parity of ML models in a query-efficient manner. We propose an optimal deterministic algorithm, as well as a practical randomized, oracle-efficient algorithm with comparable guarantees. Furthermore, we make inroads into understanding the optimal query complexity of randomized active fairness estimation algorithms. Our first exploration of active fairness estimation aims to put AI governance on firmer theoretical foundations. |
|
Outstanding Paper Runner Up
|
[ Ballroom 3 & 4 ] 
Pearl’s do calculus is a complete axiomatic approach to learn the identifiable causal effects from observational data. When such an effect is not identifiable, it is necessary to perform a collection of often costly interventions in the system to learn the causal effect. In this work, we consider the problem of designing the collection of interventions with the minimum cost to identify the desired effect. First, we prove that this prob-em is NP-complete, and subsequently propose an algorithm that can either find the optimal solution or a logarithmic-factor approximation of it. This is done by establishing a connection between our problem and the minimum hitting set problem. Additionally, we propose several polynomial time heuristic algorithms to tackle the computational complexity of the problem. Although these algorithms could potentially stumble on sub-optimal solutions, our simulations show that they achieve small regrets on random graphs. |
|
Outstanding Paper Runner Up
|
[ Hall E ] 
We propose Adversarially Trained Actor Critic (ATAC), a new model-free algorithm for offline reinforcement learning (RL) under insufficient data coverage, based on the concept of relative pessimism. ATAC is designed as a two-player Stackelberg game framing of offline RL: A policy actor competes against an adversarially trained value critic, who finds data-consistent scenarios where the actor is inferior to the data-collection behavior policy. We prove that, when the actor attains no regret in the two-player game, running ATAC produces a policy that provably 1) outperforms the behavior policy over a wide range of hyperparameters that control the degree of pessimism, and 2) competes with the best policy covered by data with appropriately chosen hyperparameters. Compared with existing works, notably our framework offers both theoretical guarantees for general function approximation and a deep RL implementation scalable to complex environments and large datasets. In the D4RL benchmark, ATAC consistently outperforms state-of-the-art offline RL algorithms on a range of continuous control tasks. |
|
Outstanding Paper Runner Up
|
[ Ballroom 3 & 4 ] 
The fast spreading adoption of machine learning (ML) by companies across industries poses significant regulatory challenges. One such challenge is scalability: how can regulatory bodies efficiently \emph{audit} these ML models, ensuring that they are fair? In this paper, we initiate the study of query-based auditing algorithms that can estimate the demographic parity of ML models in a query-efficient manner. We propose an optimal deterministic algorithm, as well as a practical randomized, oracle-efficient algorithm with comparable guarantees. Furthermore, we make inroads into understanding the optimal query complexity of randomized active fairness estimation algorithms. Our first exploration of active fairness estimation aims to put AI governance on firmer theoretical foundations. |
|
Outstanding Paper Runner Up
|
[ Hall G ] 
We consider the problem of predicting a protein sequence from its backbone atom coordinates. Machine learning approaches to this problem to date have been limited by the number of available experimentally determined protein structures. We augment training data by nearly three orders of magnitude by predicting structures for 12M protein sequences using AlphaFold2. Trained with this additional data, a sequence-to-sequence transformer with invariant geometric input processing layers achieves 51% native sequence recovery on structurally held-out backbones with 72% recovery for buried residues, an overall improvement of almost 10 percentage points over existing methods. The model generalizes to a variety of more complex tasks including design of protein complexes, partially masked structures, binding interfaces, and multiple states. |
|
Outstanding Paper Runner Up
|
[ Ballroom 1 & 2 ] 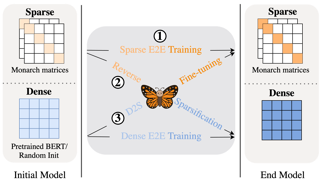
Large neural networks excel in many domains, but they are expensive to train and fine-tune. A popular approach to reduce their compute or memory requirements is to replace dense weight matrices with structured ones (e.g., sparse, low-rank, Fourier transform). These methods have not seen widespread adoption (1) in end-to-end training due to unfavorable efficiency--quality tradeoffs, and (2) in dense-to-sparse fine-tuning due to lack of tractable algorithms to approximate a given dense weight matrix. To address these issues, we propose a class of matrices (Monarch) that is hardware-efficient (they are parameterized as products of two block-diagonal matrices for better hardware utilization) and expressive (they can represent many commonly used transforms). Surprisingly, the problem of approximating a dense weight matrix with a Monarch matrix, though nonconvex, has an analytical optimal solution. These properties of Monarch matrices unlock new ways to train and fine-tune sparse and dense models. We empirically validate that Monarch can achieve favorable accuracy-efficiency tradeoffs in several end-to-end sparse training applications: speeding up ViT and GPT-2 training on ImageNet classification and Wikitext-103 language modeling by 2x with comparable model quality, and reducing the error on PDE solving and MRI reconstruction tasks by 40%. In sparse-to-dense training, with a simple technique … |
|
Outstanding Paper Runner Up
|
[ Hall E ] 
Pearl’s do calculus is a complete axiomatic approach to learn the identifiable causal effects from observational data. When such an effect is not identifiable, it is necessary to perform a collection of often costly interventions in the system to learn the causal effect. In this work, we consider the problem of designing the collection of interventions with the minimum cost to identify the desired effect. First, we prove that this prob-em is NP-complete, and subsequently propose an algorithm that can either find the optimal solution or a logarithmic-factor approximation of it. This is done by establishing a connection between our problem and the minimum hitting set problem. Additionally, we propose several polynomial time heuristic algorithms to tackle the computational complexity of the problem. Although these algorithms could potentially stumble on sub-optimal solutions, our simulations show that they achieve small regrets on random graphs. |
|
Outstanding Paper Runner Up
|
[ Hall E ] 
Large neural networks excel in many domains, but they are expensive to train and fine-tune. A popular approach to reduce their compute or memory requirements is to replace dense weight matrices with structured ones (e.g., sparse, low-rank, Fourier transform). These methods have not seen widespread adoption (1) in end-to-end training due to unfavorable efficiency--quality tradeoffs, and (2) in dense-to-sparse fine-tuning due to lack of tractable algorithms to approximate a given dense weight matrix. To address these issues, we propose a class of matrices (Monarch) that is hardware-efficient (they are parameterized as products of two block-diagonal matrices for better hardware utilization) and expressive (they can represent many commonly used transforms). Surprisingly, the problem of approximating a dense weight matrix with a Monarch matrix, though nonconvex, has an analytical optimal solution. These properties of Monarch matrices unlock new ways to train and fine-tune sparse and dense models. We empirically validate that Monarch can achieve favorable accuracy-efficiency tradeoffs in several end-to-end sparse training applications: speeding up ViT and GPT-2 training on ImageNet classification and Wikitext-103 language modeling by 2x with comparable model quality, and reducing the error on PDE solving and MRI reconstruction tasks by 40%. In sparse-to-dense training, with a simple technique … |