|
Outstanding Paper
|

Unrolled computation graphs arise in many scenarios, including training RNNs, tuning hyperparameters through unrolled optimization, and training learned optimizers. Current approaches to optimizing parameters in such computation graphs suffer from high variance gradients, bias, slow updates, or large memory usage. We introduce a method called Persistent Evolution Strategies (PES), which divides the computation graph into a series of truncated unrolls, and performs an evolution strategies-based update step after each unroll. PES eliminates bias from these truncations by accumulating correction terms over the entire sequence of unrolls. PES allows for rapid parameter updates, has low memory usage, is unbiased, and has reasonable variance characteristics. We experimentally demonstrate the advantages of PES compared to several other methods for gradient estimation on synthetic tasks, and show its applicability to training learned optimizers and tuning hyperparameters. |
|
Outstanding Paper
|
[ Virtual ] 
Unrolled computation graphs arise in many scenarios, including training RNNs, tuning hyperparameters through unrolled optimization, and training learned optimizers. Current approaches to optimizing parameters in such computation graphs suffer from high variance gradients, bias, slow updates, or large memory usage. We introduce a method called Persistent Evolution Strategies (PES), which divides the computation graph into a series of truncated unrolls, and performs an evolution strategies-based update step after each unroll. PES eliminates bias from these truncations by accumulating correction terms over the entire sequence of unrolls. PES allows for rapid parameter updates, has low memory usage, is unbiased, and has reasonable variance characteristics. We experimentally demonstrate the advantages of PES compared to several other methods for gradient estimation on synthetic tasks, and show its applicability to training learned optimizers and tuning hyperparameters. |
|
Outstanding Paper Honorable Mention
|
[ Virtual ] 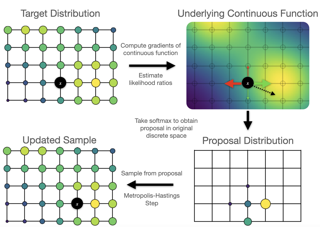
We propose a general and scalable approximate sampling strategy for probabilistic models with discrete variables. Our approach uses gradients of the likelihood function with respect to its discrete inputs to propose updates in a Metropolis-Hastings sampler. We show empirically that this approach outperforms generic samplers in a number of difficult settings including Ising models, Potts models, restricted Boltzmann machines, and factorial hidden Markov models. We also demonstrate our improved sampler for training deep energy-based models on high dimensional discrete image data. This approach outperforms variational auto-encoders and existing energy-based models. Finally, we give bounds showing that our approach is near-optimal in the class of samplers which propose local updates. |
|
Outstanding Paper Honorable Mention
|
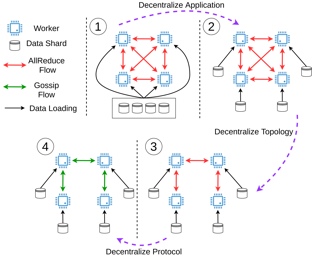
Decentralization is a promising method of scaling up parallel machine learning systems. In this paper, we provide a tight lower bound on the iteration complexity for such methods in a stochastic non-convex setting. Our lower bound reveals a theoretical gap in known convergence rates of many existing decentralized training algorithms, such as D-PSGD. We prove by construction this lower bound is tight and achievable. Motivated by our insights, we further propose DeTAG, a practical gossip-style decentralized algorithm that achieves the lower bound with only a logarithm gap. Empirically, we compare DeTAG with other decentralized algorithms on image classification tasks, and we show DeTAG enjoys faster convergence compared to baselines, especially on unshuffled data and in sparse networks. |
|
Outstanding Paper Honorable Mention
|
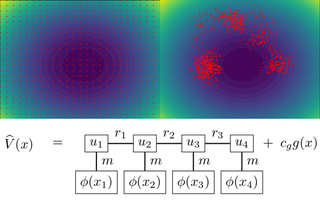
High-dimensional partial differential equations (PDEs) are ubiquitous in economics, science and engineering. However, their numerical treatment poses formidable challenges since traditional grid-based methods tend to be frustrated by the curse of dimensionality. In this paper, we argue that tensor trains provide an appealing approximation framework for parabolic PDEs: the combination of reformulations in terms of backward stochastic differential equations and regression-type methods in the tensor format holds the promise of leveraging latent low-rank structures enabling both compression and efficient computation. Following this paradigm, we develop novel iterative schemes, involving either explicit and fast or implicit and accurate updates. We demonstrate in a number of examples that our methods achieve a favorable trade-off between accuracy and computational efficiency in comparison with state-of-the-art neural network based approaches. |
|
Outstanding Paper Honorable Mention
|

High-dimensional partial differential equations (PDEs) are ubiquitous in economics, science and engineering. However, their numerical treatment poses formidable challenges since traditional grid-based methods tend to be frustrated by the curse of dimensionality. In this paper, we argue that tensor trains provide an appealing approximation framework for parabolic PDEs: the combination of reformulations in terms of backward stochastic differential equations and regression-type methods in the tensor format holds the promise of leveraging latent low-rank structures enabling both compression and efficient computation. Following this paradigm, we develop novel iterative schemes, involving either explicit and fast or implicit and accurate updates. We demonstrate in a number of examples that our methods achieve a favorable trade-off between accuracy and computational efficiency in comparison with state-of-the-art neural network based approaches. |
|
Outstanding Paper Honorable Mention
|

We propose a general and scalable approximate sampling strategy for probabilistic models with discrete variables. Our approach uses gradients of the likelihood function with respect to its discrete inputs to propose updates in a Metropolis-Hastings sampler. We show empirically that this approach outperforms generic samplers in a number of difficult settings including Ising models, Potts models, restricted Boltzmann machines, and factorial hidden Markov models. We also demonstrate our improved sampler for training deep energy-based models on high dimensional discrete image data. This approach outperforms variational auto-encoders and existing energy-based models. Finally, we give bounds showing that our approach is near-optimal in the class of samplers which propose local updates. |
|
Outstanding Paper Honorable Mention
|
[ Virtual ] 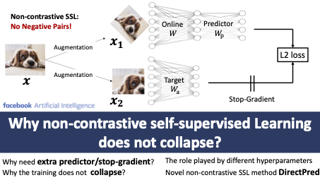
While contrastive approaches of self-supervised learning (SSL) learn representations by minimizing the distance between two augmented views of the same data point (positive pairs) and maximizing views from different data points (negative pairs), recent \emph{non-contrastive} SSL (e.g., BYOL and SimSiam) show remarkable performance {\it without} negative pairs, with an extra learnable predictor and a stop-gradient operation. A fundamental question rises: why they do not collapse into trivial representation? In this paper, we answer this question via a simple theoretical study and propose a novel approach, \ourmethod{}, that \emph{directly} sets the linear predictor based on the statistics of its inputs, rather than trained with gradient update. On ImageNet, it performs comparably with more complex two-layer non-linear predictors that employ BatchNorm and outperforms linear predictor by $2.5\%$ in 300-epoch training (and $5\%$ in 60-epoch). \ourmethod{} is motivated by our theoretical study of the nonlinear learning dynamics of non-contrastive SSL in simple linear networks. Our study yields conceptual insights into how non-contrastive SSL methods learn, how they avoid representational collapse, and how multiple factors, like predictor networks, stop-gradients, exponential moving averages, and weight decay all come into play. Our simple theory recapitulates the results of real-world ablation studies in both STL-10 and ImageNet. …
|
|
Outstanding Paper Honorable Mention
|

While contrastive approaches of self-supervised learning (SSL) learn representations by minimizing the distance between two augmented views of the same data point (positive pairs) and maximizing views from different data points (negative pairs), recent \emph{non-contrastive} SSL (e.g., BYOL and SimSiam) show remarkable performance {\it without} negative pairs, with an extra learnable predictor and a stop-gradient operation. A fundamental question rises: why they do not collapse into trivial representation? In this paper, we answer this question via a simple theoretical study and propose a novel approach, \ourmethod{}, that \emph{directly} sets the linear predictor based on the statistics of its inputs, rather than trained with gradient update. On ImageNet, it performs comparably with more complex two-layer non-linear predictors that employ BatchNorm and outperforms linear predictor by $2.5\%$ in 300-epoch training (and $5\%$ in 60-epoch). \ourmethod{} is motivated by our theoretical study of the nonlinear learning dynamics of non-contrastive SSL in simple linear networks. Our study yields conceptual insights into how non-contrastive SSL methods learn, how they avoid representational collapse, and how multiple factors, like predictor networks, stop-gradients, exponential moving averages, and weight decay all come into play. Our simple theory recapitulates the results of real-world ablation studies in both STL-10 and ImageNet. …
|
|
Outstanding Paper Honorable Mention
|

Decentralization is a promising method of scaling up parallel machine learning systems. In this paper, we provide a tight lower bound on the iteration complexity for such methods in a stochastic non-convex setting. Our lower bound reveals a theoretical gap in known convergence rates of many existing decentralized training algorithms, such as D-PSGD. We prove by construction this lower bound is tight and achievable. Motivated by our insights, we further propose DeTAG, a practical gossip-style decentralized algorithm that achieves the lower bound with only a logarithm gap. Empirically, we compare DeTAG with other decentralized algorithms on image classification tasks, and we show DeTAG enjoys faster convergence compared to baselines, especially on unshuffled data and in sparse networks. |